A projectről:
Ezt a fordulatszámmérőt egy modell termoakusztikus motor teljesítményméréséhez készítem.
A modell termoakusztikus motorról:
Ez egy hőlégmotor, ami hasonlatosan kívülről melegített motor, mint a gőzgép, de nem gőz a munkaközege, hanem gáz, illetve játékmodell esetén levegő, ami a melegítés hatására kitágul, a hűtéstől pedig összehúzódik, és így a levegő, és nem a gőz térfogatváltozása működteti a gépet.
A hőlégmotorokról:
https://en.wikipedia.org/wiki/Hot_air_engine
A stirling ciklusú hőlégmotorokról:
https://stirlingtechnology.blogspot.com/
és a termoakusztikus hőlégmotorokról itt olvashatsz bővbben:
https://tibsim-thermoacoustics1488.blogspot.com/
Nagyon leegyszerűsítve, az adott termoakusztikus motor a következőképpen működik.
Van egy kémcső, amelybe a zárt végétől kb. az egy harmadáig belerakunk egy laza állagú fémgyapotot, amit a festők is használnak, tehát festékboltban is kapható. Ennek a pár cm hosszú fémvattának a neve stack. A stacknek a kémcső zárt vége felöli oldalát melegítjük egy alkoholos égő lángjával, a másik végét, a kémcső nyitott oldala felőlit pedig hűtjük, mégpedig úgy, hogy a kémcsőre ott egy kis darab nedves papírzsebkendő darabot rátekerünk. A kémcsőbe a levegő rezonálni képes, mivel a gáznak van tömege és rugalmassága, úgy rezeg a félig nyitott kémcsőbe, mintha dugattyú lenne. Amikor a kémcsőbe befelé lendül a gázdugattyú, akkor fémvatta hideg oldalából a gáz a meleg oldalába kerül, ott egy kis időkéséssel felmelegszik, kitágul, és a gázdugattyút a nyitott vég, illetve a légkör irányába lendíti. Ekkor viszont a stack meleg oldalában lévő gáz a hideg oldalba kerül, ott lehűl, összehúzódik, részleges vákuum keletkezik, és a légköri nyomás a légdugattyút a kémcsőbe lendíti vissza. Ez ismétlődik a kémcső méreteiből adódó rezonancia frekvencián, és mivel ez általában kémcső méretben halható hangfrekvencia, ezért hangos (95-100 db) sípolást érzékelhetünk.
https://www.youtube.com/watch?v=3qd_tuLwCRg
Mivel a gáz kifelé sokkal inkább egyirányúan, előrefelé áramlik, míg befelé a kémcsőbe sokkal inkább oldal irályból, a kémcső szájánál szélszerű fújást illetve szélszerű jelenséget tapasztalhatunk. Ezt a fújást irányítjuk egy egyszerű turbinakerékre, és ennek a gépnek mérjük le a teljesítményét. Videó a projectről:
Még annyit, hogy a gép geometriáját a jobb fújás érdekében némileg változtattam, a rezonátor cső vékonyabb, a gép hosszát megnöveltem, a frekvenciája és a hangossága sokkal alacsonyabbra van így állítva, de jobban fúj. Ha mélyebben bele akarsz merülni, ezen az oldalon olvashatsz róla:
https://tibsim-thermoacoustics1488.blogspot.com/p/types.html
A fékpad:
A prony-pad egy fékpad vagy másképpen mérőpad, amellyel a különböző típusú motoroknak a teljesítményét megmérhetjük, és itt gondolhatunk a gőzgéptől a modern gépjármű motorokig.. Én most a már említett állóhullámú termoakusztikus generátor modell turbinájának teljesítményét mérem majd meg vele.
Ennek a turbinakerékkel rendelkező motornak, egy fékpaddal (prony-paddal ) megmérem a nyomatékát, majd fordulatszámát, ezeket összeszorozva kiszámolom a teljesítményét, és az eredményt összehasonlítva az elektromos generátorának az adataival, meghatározhatjuk annak a hatásfokát is. Valószínűleg az elektromos generátor a graetz egyenirányító hídon veszíti majd el a hatásfokának, és teljesítményének nagy részét. Ennek a vizsgálata majd később, a project folytatása lesz.
Felépítés:
A prony padhoz készítek egy, a tengelyen csúszó, surlódó fékpofaszerkezetet, és megmérem az erőt, amit a fékpad fejt ki a mérlegre . A fékpofaszerkezetet úgy kell elkészíteni, hogy vagy szimmetrikus illetve kiegyensúlyozott legyen, és a tömegközéppontja a turbina tengelyén legyen, és így önmaga ne gyakoroljon nyomást a mérlegre vagy, és ezt fogom használni, a mérlegen megmérem a prony-pad által a motor nyugalmi állapotában kiejtett erőt, és a számításba kalkulálom, vagyis kivonom abból az adatból, amikor a motor működik
Nyilvánvalóan, a turbina teljesítményének karakterisztikájára romboló hatása van a fordulatszám esése, azaz különböző fordulatszámokon különböző a teljesítmény, lassabb esetén kisebb, ezért a fékpofaszerkezet súrlódását úgy állítom be, hogy a turbina ne veszítsen sokat a sebességéből. Hogy minél pontosabb legyen a teljesítmény mérése, ezért szükséges, hogy a mérleg kellően érzékeny legyen, és mivel kis teljesítményt mérünk, a mérlegre támaszkodó fékpofa (erő) karját is rövidre érdemes elkészíteni.
A turbina fordulatszámát pedig az alább kifejtett arduinoval mérem közben.
A teljesítmény kiszámítása:
Először megmérem a fékpofa súlyát úgy, hogy a hőerőgép nyugalmi állapotban van, tehát nem működik, és ezt majd kivonom abból az erőből, amit akkor mérek, amikor a forgó turbina nyomja majd a mérleget. Ha ismerem a nyomatékkar hosszát (= L), és a fordulatszámot is (N = RPM vagy igazából másodpercben RPS, mert inkább arra van szükségünk a képletben), akkor kiszámolhatjuk a teljesítményt!
A teljesítmény (= P) definíciója az egységnyi idő alatt végzett munka, vagyis a kifejtett erő szorzata a távolsággal.
Lásd még:
https://www.instructables.com/Design-criteria-for-Stirling-cycle-engine/
stb.stb.
Az arduino fordulatszámmérő:
Az arduino kódját úgy terveztem meg, hogy minden 10. fordulat után számolja, és írja ki az eredményt RPM-be. Így szerintem pontosabb, de az adatfrissítés sűrűsége még ideális is, mivel a turbina nem lesz túl gyors. Nem csak az LCD kijelzőre, hanem a sorosmonitorra is kiíratom a eredményt.
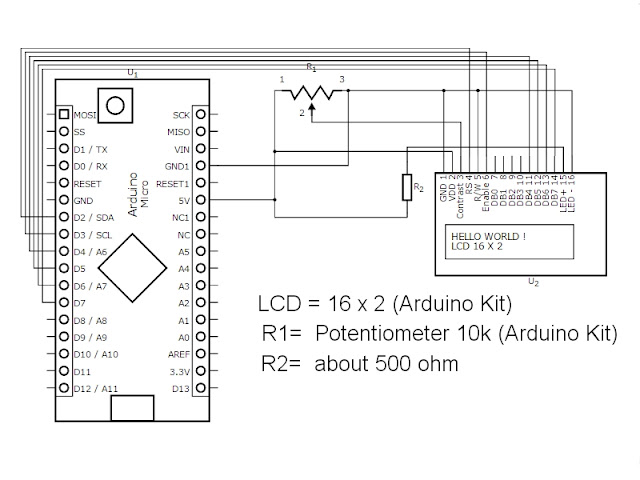
Az LCD display bekötése:
A LED-ek bekötése:
Az arduino kódja:
#include <LiquidCrystal.h>
LiquidCrystal lcd(2, 3, 4, 5, 6, 7);
int situation = 1;
int counter = 0;
int comparative = 0;
unsigned long time1 = 0;
unsigned long time2 = 0;
unsigned long rpm = 0;
void setup() {
pinMode(13, OUTPUT);
//visitor's lighthouse
pinMode(11, INPUT);
digitalWrite(11, HIGH);
//sensors
pinMode(10, OUTPUT);
digitalWrite(10, 1);
// IR radiate You can use two from it also.
lcd.begin(16, 2);
lcd.setCursor(0,1);
lcd.clear();
lcd.print("Hello");
Serial.begin(9600);
}
void loop() {
if (digitalRead(11) == HIGH){
situation = 1;
}
if (digitalRead(11) == LOW){
situation = 2;
}
if(situation != comparative){
if (situation == 1){
counter = counter + 1;
digitalWrite(13, LOW);
}
if (situation == 2){
digitalWrite(13, HIGH);
}
if (counter == 0){
time1 = millis();
}
if (counter == 10){
time2 = millis() - time1;
rpm= 600000 / time2;
Serial.println(rpm);
lcd.clear();
lcd.print("RPM =");
lcd.print(rpm);
counter = 0;
}
}
comparative = situation;
}
A mérleg:
Max. 200 grammot mér 0.01 gramm pontossággal. 1723 Ft.
Teljesítmény mérése multiméterrel (feszültség és áramerősség mérővel):
Itt most a hatásos teljesítményre vagyunk kíváncsiak, vagyis a tényleges munkát végző teljesítményre, és nem foglalkozunk a látszólagos, és meddő teljesítmény témakörével!
Teljesítmény jele: P mértékegysége W (watt)
Áramerősség jele: I mértékegysége A (amper)
Feszültség jele: U mértékegysége V (volt)
A generátorunk egy fázisú, szinuszos váltóáramot generál, ezért két módszer jöhet számításba a teljesítményének a megméréséhez.
1. Átalakítjuk egyenárammá, és akkor:
P = U * I vagy ebben az esetben lehet
P = (U * U) / R használni is.
Amire még szükségünk lehet a jobb megértéshez:
R = U/I
Egyenárammá greatz-híddal, és kondenzátorral tudjuk átalakítani a váltóáramot így:
http://www.creative-science.org.uk/gensimple2.html
2.Vagy nem alakítjuk át, és RMS (Root Mean Square = négyzetes középérték) teljesítményt számítunk.
Ebben az estben is, a váltakozó feszültségű áramból egyenfeszültségűt "csinálunk", de nem gyakorlatilag, hanem matematikailag.
Mivel a generátorunk egy fázisú, és ohmos ellenálláson mérünk, nincs jelen jelentős kapacitív (kondenzátoros) vagy induktív (tekercs) ellenállásunk, így az áramkörünkben a feszültség és az áramerősség is egy fázisban van, ezért a teljesítmény is szinuszosan változik, és egyszerűen megmérhetjük, kiszámolhatjuk az effektív teljesítményt.
Az effektív (hatásos) teljesítmény adatunk a szinuszosan váltakozó teljesítményünk egy olyan középértéke, ami megfelel az egyenáram munkavégző értékével. Egyszerűbben, matematikailag a szinuszos váltakozó teljesítményt átváltjuk egy egyenáramú teljesítményre.
A szinuszos azt jelenti, hogy generátor forgásából adódóan egyenletesen változik az érték, ezért egyszerű matematikai képlettel számolható, de most nincs szükségünk arra, hogy ezzel bővebben itt foglalkozzunk. Amúgy össze-vissza is változhat, pl hangfrekvencia esetén, de szerencsére itt nem erről van szó.
A multiméteren lehetőség van váltakozó szinuszos feszültség mérésére, és nem kell számolnunk, mert ez már egy RMS feszültségadatot közöl, vagyis nem a feszültség csúcsmértékét, hanem egy egyenáramnak megfelelő középértéket ad meg, amit egyenirányított középértéknek neveznek.
( Pl a hálózati feszültségünk, a 230V és ez egy RMS adat, a csúcsfeszültsége 324V. Azért elárulom, de itt nincs rá szükség, hogy az RMS-t úgy kapjuk meg egy szinuszosan váltakozó feszültség esetében, hogy a csúcsfeszültséget megszorozzuk 0.71-el. Ez a helyzet az áramerősség tekintetében is, de a multimétereken általában csak váltakozó feszültséget lehet mérni, áramerősséget nem.)
Mivel ismerjük az ohmos ellenállásunk értékét, így a képlet a következő lesz:
P = ( U * U ) / R
Lásd még, ha bővebben érdekel:
Ami még fontos:
A generátorunk teljesítmény mérésénél gyakorlatilag azt mérjük, hogy az ellenállásunk mekkora teljesítményt vesz fel, ezért egy pótmétert, azaz állítható ellenállást kapcsolunk a generátorra, és az ellenállás változtatásával tudjuk megkeresni a multiméter(ek) adataiból, hogy hány ohmnál számolhatjuk a legnagyobb teljesítményt, amikor a feszültséget és áramerősséget összeszorozzuk, vagy egyszerűen egy adott ellenállásmértéken számoljuk, de az nyilván kevésbé lesz pontos.
-------------------
Itt átalakítottam frekvenciaszámlálóra a fenti kódot, ami sorosmonitoron adja Hz-ben a frekvenciát.
7000Hz-ig biztosan, és jól működött, 11000Hz-nél akadozott a próbapanel érintkezési hibái nem tetszett neki. 1Hz alatti értéket is mér, de vedd figyelembe, hogy 100 jelenként írja ki a frekvenciát. Vagyis 1Hz-nél 100 másodpercenként, 10000Hz -nél 0,1 másodpercenként.
int situation = 1;
int counter = 0;
int comparative = 0;
unsigned long time1 = 0;
unsigned long time2 = 0;
unsigned long hz = 0;
void setup() {
pinMode(11, INPUT);
digitalWrite(11, HIGH);
Serial.begin(9600);
}
void loop() {
if (digitalRead(11) == HIGH){
situation = 1;
}
if (digitalRead(11) == LOW){
situation = 2;
}
if(situation != comparative){
if (situation == 1){
counter = counter + 1;
}
if (situation == 2){
}
if (counter == 0){
time1 = micros();
}
if (counter == 100){
time2 = micros()- time1;
hz = 100000000 / time2;
Serial.println(hz);
counter = 0;
}
}
comparative = situation;
}